The Mathematics Pentathlon® Program provides experiences in thought processes necessary for Active Problem Solving. The series of 20 Mathematics Pentathlon games provide K-7 students with experiences in deductive and inductive reasoning through the repeated use of sequential thought as well as nonlinear, intuitive thinking. Exposure to such forms of thought helps students relate to real-life problem-solving situations and learn to “think on their feet.”
The Four Sections below explain the following: Active Problem Solving Defined, What is Mathematics, Three Types of Mathematical Thought, and Conceptual Understanding Using Concrete and Pictorial Models.
SECTION 1
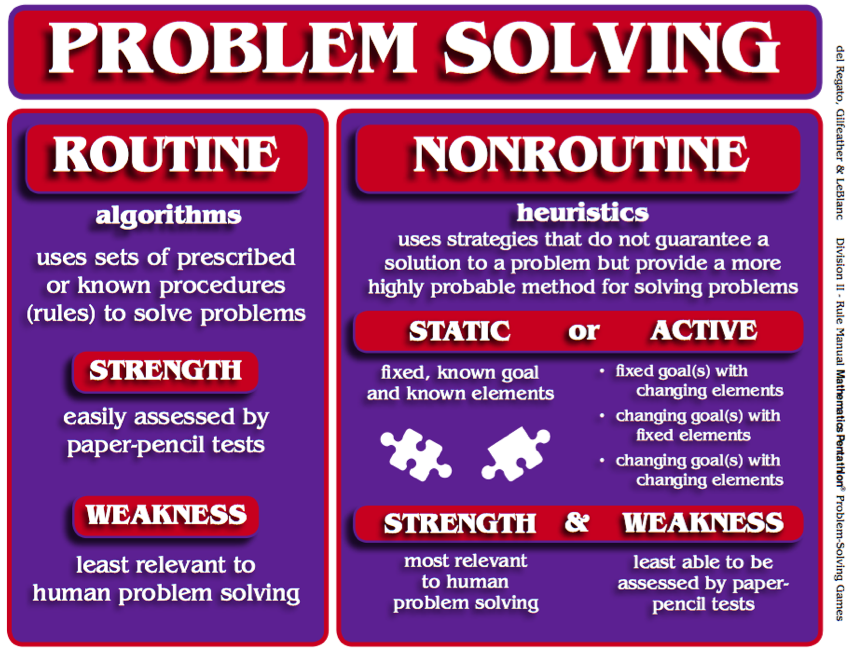
Problem Solving Can Be Divided Into Two Categories:
Routine & Non-Routine
Routine Problem Solving, stresses the use of sets of known or prescribed procedures (algorithms) to solve problems. The strength of this approach is that it is easily assessed by paper-pencil tests. Since today’s computers and calculators can quickly and accurately perform the most complex arrangements of algorithms for multi-step routine problems, the typical workplace does not require a high level of proficiency in Routine Problem Solving. However, today’s workplace does require many employees to be proficient in Nonroutine Problem Solving.
Nonroutine Problem Solving, stresses the use of heuristics and often requires little to no use of algorithms. Unlike algorithms, heuristics are procedures or strategies that do not guarantee a solution to a problem but provide a more highly probable method for discovering a solution. Building a model and drawing a picture of a problem are two basic problem-solving heuristics. Studying end-of-game situations provides students with experiences in using the heuristics of reducing the problem to a similar but simpler problem and working a problem backwards, i.e. from its resolution to its initial state. Other heuristics include describing the problem situation, classifying information, and finding irrelevant information.
There Are Two Categories of Nonroutine Problem Solving:
Static and Active
Static-Nonroutine problems have a fixed, known goal and fixed, known elements that are used to resolve the problem. Solving a jigsaw puzzle is an example of a Static- Nonroutine problem. Given all pieces to a puzzle and a picture of the goal, learners are challenged to arrange the pieces to complete the picture. Various heuristics such as classifying the pieces by color, connecting the pieces that form the border, or connecting the pieces that form a salient feature to the puzzle, such as a flag pole, are typical ways in which people attempt to resolve such problems.
Active-Nonroutine problems may have a fixed goal with changing elements, a changing goal or alternative goals with fixed elements, or changing or alternative goals with changing elements. The heuristics used in this form of problem-solving are known as strategies. People who study such problems must learn to change or adapt their strategies as the problem unfolds.
SECTION 2
There is a growing belief in the mathematics community, as well as society in general, that the study of mathematics must develop in all students an understanding of mathematics that continues throughout one’s lifetime and evolves to meet ever-changing situations and variables. From our perspective, mathematics is an area of investigation that develops the ability to critically observe, classify, describe, and analyze data in a logical manner using both inductive and deductive methods. In contrast to the sterilized and unrelated manner in which school mathematics has often been taught, mathematics is a creative and aesthetic study of patterns and geometric and numerical relationships. It is dynamic rather than passive in nature and should involve students in strategic thinking by exploring multiple possibilities and variables that continually change, much like life.

The Mathematics Pentathlon® Program, which integrates Adventures in Problem Solving, Activity Books I & II, the Mathematics Pentathlon® Games and Investigation Exercises, Books I & II was designed to implement the definition of mathematics described above. The games are organized into four division levels by grade, K-1, 2-3, 4- 5, and 6-7 with five games at each level. The name of the Program, Mathematics Pentathlon®, was coined to liken it to a worldwide series of athletic events, the Decathlon component of the Olympics. In the world of athletics the Decathlon is appreciated for valuing and rewarding individuals who have developed a diverse range of athletic abilities. In contrast, the mathematics community as a whole has rarely valued or rewarded individuals with a diverse range of mathematics abilities. The Mathematics Pentathlon® Games promote diversity in mathematical thinking by integrating spatial/ geometric, arithmetic/computational, and logical/scientific reasoning at each division level. Since each of the 5 games requires students to broaden their thought processes, it attracts students from a wide range of ability levels, from those considered “gifted and talented” to “average” to “at-risk.”

The format of games was chosen for two reasons. First, games that are of a strategic nature require students to consider multiple options and formulate strategies based on expected countermoves from the other player. The Mathematics Pentathlon® further promotes this type of thought by organizing students into groups of four and teams of two. Teams alternate taking turns and team partners alternate making decisions about particular plays by discussing aloud the various options and possibilities. In this manner, all group members grow in their understanding of multiple options and strategies. As students play these games over the course of time, they learn to make a plan based on better available options as well as to reassess and adjust this plan based on what the other team acted upon to change their prior ideas. Through this interactive process of sharing ideas and possibilities, students learn to think many steps ahead, blending both inductive and deductive thinking. Second, games were chosen as a format since they are a powerful motivational tool that attracts students from a diverse range of abilities and interest levels to spend more time on task developing basic skills as well as problem-solving skills. While race-type games based on chance are commonly used in classrooms, they do not typically capture students’ curiosity for long periods of time. Students may play such games once or twice, but then lose interest since they are not seriously challenged. The Mathematics Pentathlon® Games have seriously challenged students to mature in their ability to think strategically and resolve problems that are continually undergoing change. As a result, we view active-problem solving and strategic thinking as described above as a critical focal point of the mathematics curriculum.
SECTION 3
Integration of Spatial/Geometric, Computational,
and Logical/Scientific Reasoning
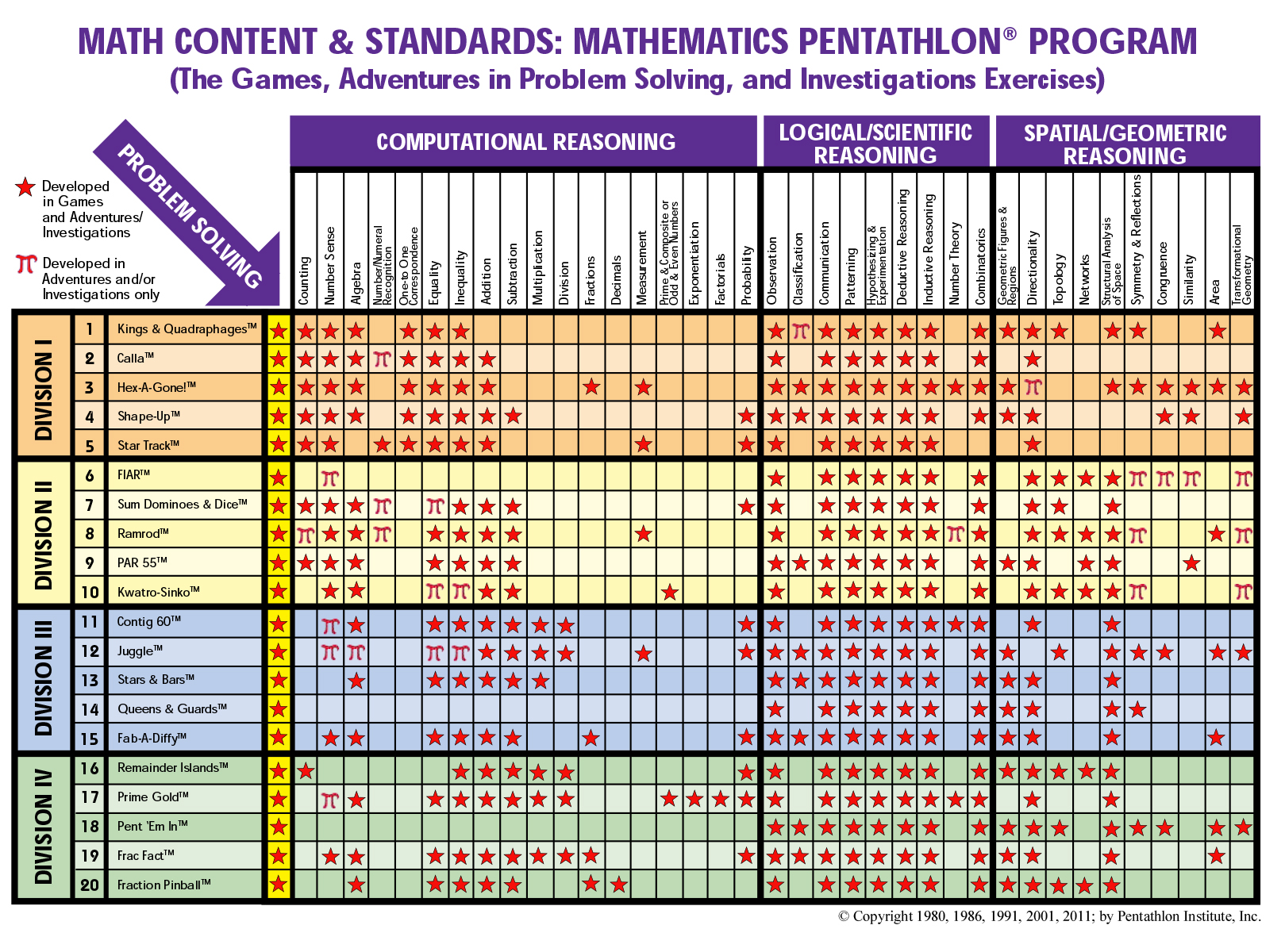
Most mathematics instruction stresses students’ knowledge of basic arithmetic facts. While the Mathematics Pentathlon Program provides a great deal of practice with mastery of the basic facts, it goes far beyond learning arithmetic skills. The Mathematics Content and Standards Chart for the 20 Mathematics Pentathlon Games shows how each game addresses several mathematical content and process objectives (see inside back cover of manual). These objectives have been clustered into logical/scientific reasoning, computational reasoning, and spatial/geometric reasoning. Each of these categories is described below.
Spatial/Geometric Reasoning

Spatial visualization involves the ability to image objects and pictures in the mind’s eye and to be able to mentally transform the positions and examine the properties of these objects/pictures. A large body of mathematics research concludes that spatial reasoning ability is highly related to higher-level mathematical problem-solving and geometric skills as well as students’ overall achievement in mathematics. Many of the Mathematics Pentathlon Games stress spatial reasoning and several integrate this form of thinking with logical and computational reasoning.
Computational Reasoning

Many of the Mathematics Pentathlon Games incorporate computation into the game structure. More time-on-task practicing arithmetic skills does indeed result in students’ increased performance in the classroom as well as on standardized tests. But in the Mathematics Pentathlon Games that stress computation, it is not sufficient to rely on arithmetic skills alone. To be successful in these games, students must also use their logical reasoning abilities to consider several options and to decide which ones will maximize their ability to reach the game’s goal(s).
Logical/Scientific Reasoning
One of the most important life skills, not to mention mathematical skills, is the ability to think logically. The process of observation, classification, hypothesizing, experimentation, and inductive and deductive thought are required for logical reasoning. Yet where do children learn these fundamental life skills? Strategic games provide students the opportunity to develop this form of thinking. Each of the Mathematics Pentathlon Games is a strategy game that develops students’ logical reasoning skills through the process of investigating a variety of options and choosing better options. At the same time students develop scientific reasoning skills by learning how to be better observers of game-playing variables and options. Playing the games over the course of time allows for hypothetical reasoning to evolve since students analyze sequences of “if-then” situations and make choices based on linking inductive and deductive thought.
While each of the 20 games may stress one form of the mathematical thinking over another, each game integrates at least two categories of mathematical thinking. Furthermore, the five games at each Divisional level balance the three types of reasoning.
SECTION 4
Since its inception, the National Council of Teachers of Mathematics (NCTM) has called for a conceptually-based curriculum in schools throughout the country. The most recent psychological and educational research has shown that conceptual understanding is a key attribute of individuals who are proficient in mathematics. Furthermore, a large body of research over the last four decades suggests that effective use of physical and pictorial models of mathematics concepts improves students’ conceptual understanding, problem-solving skills, and overall achievement in mathematics. Research also indicates that the use of concrete and pictorial models improves spatial visualization and geometric thinking.
The Mathematics Pentathlon® Program incorporates a variety of concrete and pictorial models to develop students’ conceptual understanding of many important mathematics concepts that involve computational, spatial, and logical reasoning. In addition, by playing these games in cooperative groups, as suggested in this publication, students also improve their oral and written communication skills through their discussion of mathematical ideas and relationships.