Integration of Spatial/Geometric, Computational,
and Logical/Scientific Reasoning
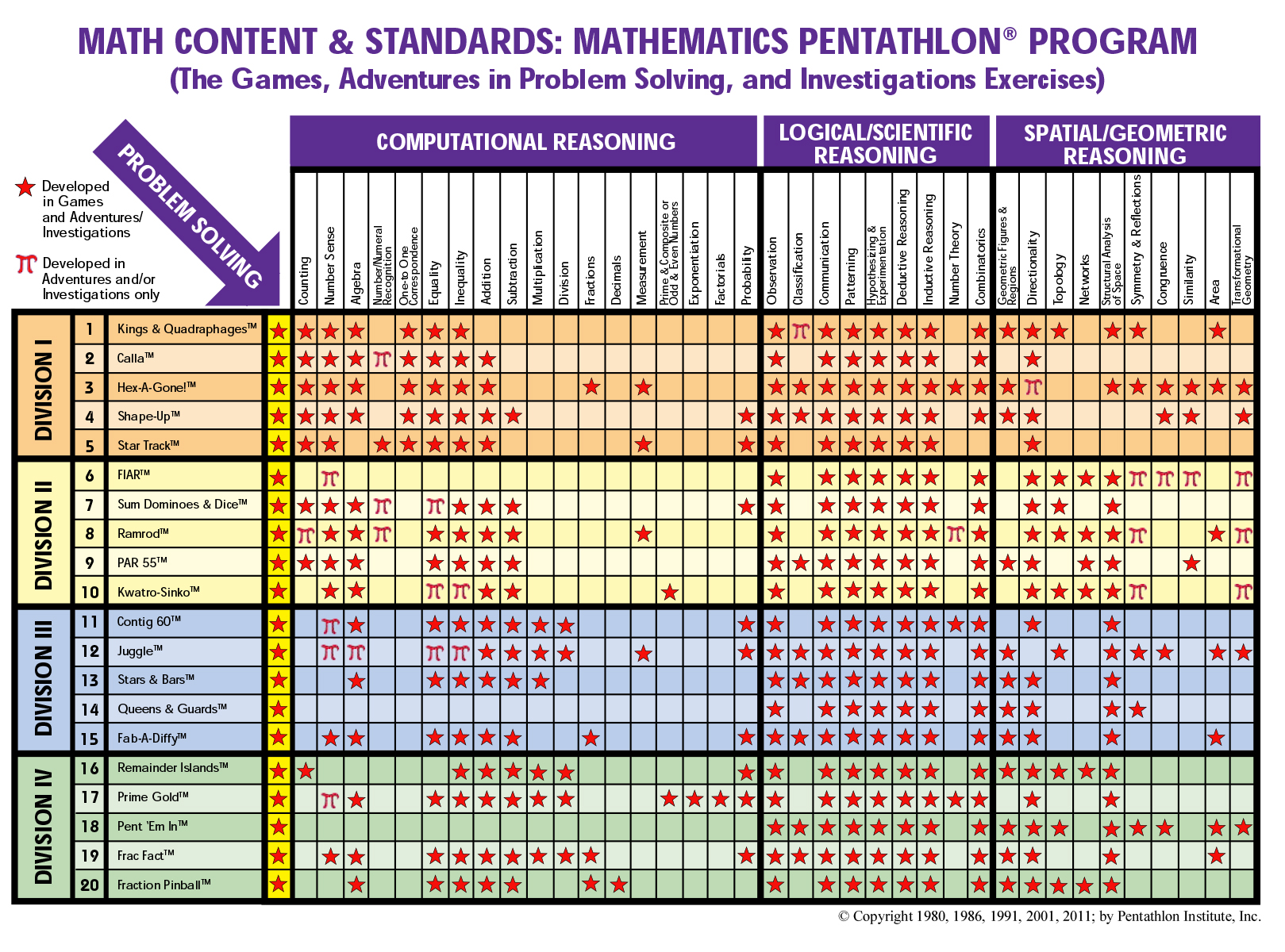
Most mathematics instruction stresses students’ knowledge of basic arithmetic facts. While the Mathematics Pentathlon Program provides a great deal of practice with mastery of the basic facts, it goes far beyond learning arithmetic skills. The Mathematics Content and Standards Chart for the 20 Mathematics Pentathlon Games shows how each game addresses several mathematical content and process objectives (see inside back cover of manual). These objectives have been clustered into logical/scientific reasoning, computational reasoning, and spatial/geometric reasoning. Each of these categories is described below.

Spatial/Geometric Reasoning
Spatial visualization involves the ability to image objects and pictures in the mind’s eye and to be able to mentally transform the positions and examine the properties of these objects/pictures. A large body of mathematics research concludes that spatial reasoning ability is highly related to higher-level mathematical problem-solving and geometric skills as well as students’ overall achievement in mathematics. Many of the Mathematics Pentathlon Games stress spatial reasoning and several integrate this form of thinking with logical and computational reasoning.

Computational Reasoning
Many of the Mathematics Pentathlon Games incorporate computation into the game structure. More time-on-task practicing arithmetic skills does indeed result in students’ increased performance in the classroom as well as on standardized tests. But in the Mathematics Pentathlon Games that stress computation, it is not sufficient to rely on arithmetic skills alone. To be successful in these games, students must also use their logical reasoning abilities to consider several options and to decide which ones will maximize their ability to reach the game’s goal(s).

Logical/Scientific Reasoning
One of the most important life skills, not to mention mathematical skills, is the ability to think logically. The process of observation, classification, hypothesizing, experimentation, and inductive and deductive thought are required for logical reasoning. Yet where do children learn these fundamental life skills? Strategic games provide students the opportunity to develop this form of thinking. Each of the Mathematics Pentathlon Games is a strategy game that develops students’ logical reasoning skills through the process of investigating a variety of options and choosing better options. At the same time students develop scientific reasoning skills by learning how to be better observers of game-playing variables and options. Playing the games over the course of time allows for hypothetical reasoning to evolve since students analyze sequences of “if-then” situations and make choices based on linking inductive and deductive thought.
While each of the 20 games may stress one form of the mathematical thinking over another, each game integrates at least two categories of mathematical thinking. Furthermore, the five games at each Divisional level balance the three types of reasoning.